Calculs de Doses - Les prérequis aux calculs de doses infirmiers

Vous êtes à l'Institut de Formation en Soins Infirmiers ou vous allez le rejoindre et vous souhaitez en savoir plus sur les prérequis pour être prêt(e) à aborder les calculs de doses ? 

 ...On vous dit tout dans cet article ! 

Le programme de la formation en soins infirmiers

Lors des trois années d’étude d’infirmière, un enseignement spécifique sur les calculs de doses est assuré dans le cadre des Unités d'enseignement 4.4 Thérapeutiques et contribution au diagnostic médical et 2.11 Pharmacologie et thérapeutiques du semestre 2 au semestre 5.

Déjà dans des unités d'enseignement complexes, les mathématiques et calculs de doses sont des notions créant une grande appréhension aussi bien chez les étudiants que chez les formateurs qui rencontrent certaines limites dans la transmission d’une pratique beaucoup plus complexe qu’elle n’apparaît de prime abord ; C'est pourquoi nous mettons en avant les prérequis aux calculs de doses nécessaires pour débuter cette discipline.

Rappel : Le référentiel est articulée de 36 matières et de 59 unités d’enseignement (UE) regroupées sous 10 compétences permettant une approche globale de la formation menant au Diplôme d’Etat Infirmier (DEI). Une compétence se définit comme un ensemble de savoirs, savoirs-être et savoirs-faire (stages). Ainsi lors de votre formation, vous devrez acquérir les 10 compétences en lien avec le métier d’infirmier-ère. Le programme de formation à l’IFSI, sur une durée de 3 années divisée en 6 semestres, répond aux référentiels d’activités, de compétences et de formation (arrêté du 31 juillet 2009 modifié relatif au diplôme d’état infirmier)

Dans le cadre pédagogique des calculs de doses, mais aussi lors des stages infirmiers, nous pouvons identifier 4 compétences, toutes indispensables pour la pratique quotidienne infirmière :

• Identifier et maîtriser les notions de dosage, de dilution et de préparation d'un thérapeutique.
• Connaître les dosages, préparations, prélèvements, débits, dilutions, solvants et solutés.

• Planifier et adapter un traitement selon la prescription du médecin.

• Etre en capacité d'effectuer aussi bien des calculs simples que complexes.

Apprendre à maîtriser les mathématiques en soins infirmiers peut être un défi, mais c'est un indispensable pour valider le diplôme mais surtout pour vos patients.

Le calcul de doses médicamenteuses est réalisé par l’infirmier dans le cadre de son rôle sur prescription pour administrer un traitement à un patient. Le calcul de dose est essentiel à la préparation d’un médicament et il doit être réalisé de façon sûre et efficace, quels que soient le lieu, le moment, les conditions et la personne qui l’effectue car toute erreur peut nuire à la qualité du soin et à l'état de santé du patient.

Le calcul de dose peut se découper en deux étapes : la première consiste à analyser le dosage mis à disposition par la pharmacie au regard de la prescription, et la seconde à adapter ce dosage spécifiquement au patient (la dose).

Les calculs de doses sont une préoccupation de l’ensemble de l’équipe médicale et paramédicale. Cette activité doit générer le minimum de risques afin de prévenir les événements indésirables liés aux soins. Dans ce cadre, le calcul de doses doit être une pratique comprise de tous, il n'y a pas de place pour le doute. 

Le calcul de dosage est une opération mathématique qui nécessite un certain nombre de prérequis mathématiques qui seront présentés ci-dessous, puis des notions de bases en calculs de doses pour arriver à un usage complexe de calculs de doses de PSE, Pompe PCA, ... avec des prélèvements de volume, dilution, débits...

Il existe ainsi un certain nombre de facteurs de risque dissimulés derrière une pratique quasi automatisée lorsqu’elle concerne des traitements habituels ou prescrits quotidiennement d'un service particulier.

Voici une liste non exhaustive des conséquences d'une erreur de calculs de doses :

• Erreur de dose : dose supplémentaire, sous dosage ou surdosage.
• Erreur d'obstination : Administration alors que les indications et/ou calculs sont non maîtrisés.
• Erreur de durée : Intervalle par prise ou par 24h non respecté.
• Erreur de débit : Débit trop long ou trop lent.
• Erreur de lecture : lecture d'une mauvaise unité ou quantité prescrite.

Dans cet article, je vous propose d'aborder les prérequis aux calculs de doses, première étape vers la maîtrise générale des calculs de doses dans les soins infirmiers, dans votre quotidien de futur diplômé.

Désormais, rentrons en détails dans les notions à bien maîtriser avant d'aborder les calculs de dose durant votre formation en soins infirmiers...

Pour cela je vous propose d'aborder les notions une par une, vous constaterez que ce sont les notions normalement vues au niveau baccalauréat, qui parfois paraissent simples, vous serons très utiles en tant que prérequis aux calculs de doses. Vous n'aurez pas le temps de revenir sur ces notions à l'IFSI, ça commencera directement fort ! 

Les calculs algébriques (Niveau 1)

C'est la base de tout calculs mathématiques, aussi appelé calcul littéral, les calculs algébriques combinent lettres et nombre dans des opérations ; Ainsi on utilise des lettres pour désigner des variables telles a, b, x et y.

Il permet de prouver une théorie, de démontrer ou de définir des lois de manière plus générale.

1. Règles de signes & parenthèses

La première chose à faire en calcul algébrique, comme habituellement dans les calculs, c'est de supprimer les parenthèses, pour cela il y a des règles spécifiques selon le signe devant : 

Signe + : Lorsque les parenthèses sont précédées du signe +, on peut les supprimer en conservant les signes qui se trouent dedans.

A = 15 + ( 5 + 20 + X ) = 15 + 5 + 20 + X

Signe - : Lorsque les parenthèses sont précédées du signe -, on peut les supprimer en inversant les signes qui se trouent dedans

B = 30 - ( 20 + X - Y ) = 30 - 20 - X + Y

2. Calculs & Simplifications de formes algébriques

Dès que les parenthèses sont enlevées, on va chercher s’il est possible de simplifier notre suite algébrique. Pour cela, nous allons pouvoir calculer les termes identiques : les nombres simples entre eux, les nombres littéraux de même facteur (lettre identique).

Pour réduire notre forme algébrique, nous allons la transformer dans l'objectif d'avoir moins de termes : 

A = 15 + ( 5 + 20 + X ) = 15 + 5 + 20 + X = 40 + X

B = 30 - ( 20 + X - Y ) = 30 - 20 - X + Y = 10 - X + Y 

NB : Cours ciblé uniquement sur les notions utiles ; L’algébrique part encore plus loin... !

Les calculs fractionnaires

Une fraction est un moyen d'écrire un nombre rationnel sous la forme d'un quotient de deux entiers. 

La fraction désigne le quotient de « a » par « b » où a est appelé le numérateur et b le dénominateur.

1. Simplifier une fraction

Simplifier une fraction, c'est l'écrire avec un numérateur et un dénominateur le plus petit. En pratique, cela revient à diviser le numérateur et le dénominateur par un même nombre. 

A = 300 ÷ 700 = (300 :100) ÷ (700 ∶100) = 3 ÷ 7

B = 24 ÷ 16= (24∶ 8) ÷ (16∶ 8) = 3 ÷ 2

NB : La division par nombre commun ne peut jamais donner un résultat décimal.

2. Inverse d'une fraction

Si a et b sont deux nombres non nuls, alors :  I = (a ÷ b ) x (b ÷ a ) = (a x b ) ÷ (b x a ) = ab ÷ ba = 1

Exemple : L’inverse du nombre −3 ÷ 7 est −7 ÷ 3

3. Additions & Soustractions de fractions

Les règles de calcul de l’addition et la soustraction sont les mêmes :

1. Avoir un dénominateur commun.
2. Additionner ou soustraire uniquement le numérateur : on conserve le dénominateur commun.

Exemples : 

A = (3 ÷ 7) + (1 ÷ 7) = (3+1) ÷ 7 = 4 ÷ 7 

B = (3 ÷ 5) + (1 ÷ 10) = (3 𝑥2 ÷ 5 𝑥2) + (1÷ 10) = (6÷ 10) + (1÷ 10) = (6+1) ÷ 10 = 7 ÷ 10

4. Multiplications

Pour multiplier deux nombres en écriture fractionnaire, on multiplie les numérateurs et les dénominateurs entre eux.

Si a, b, c et d sont quatre nombres sachant que b et d sont non nuls, alors : 

M = (a ÷ b ) x (c ÷ d ) = (a x c ) ÷ (b x d ) 

Exemples :
M1  = (7 ÷ 5) x (3 ÷ 5) = (7 x 3) ÷ (5 x 5) = 21 ÷ 25

5. Divisions

Pour diviser deux nombres en écriture fractionnaire, on multiplie le dividende par l'inverse du diviseur. 

Si a, b, c et d sont quatre nombres où b, c et d sont non nuls, alors : 

D = (a ÷ b ) : (c ÷ d ) = (a ÷ b ) x (d ÷ c )

Exemples :
D1 = (7 ÷ 5) : (2 ÷ 3) = (7 ÷ 5) x (3 ÷ 2) = (7 x 3) ÷ (5 x 2) = 21 ÷ 10

6. Calculs sous forme fractionnaires

Pour réaliser les calculs, les règles sont similaires calculs classiques : 

1. Ce qui se trouve entre côte et entre parenthèse.
2. Réaliser les multiplications et divisions en priorité.
3. Réaliser les additions et soustractions.
4. Simplification de la fraction obtenue. 

On utilise des multiples communs aux dénominateurs et numérateurs.

Exemples :

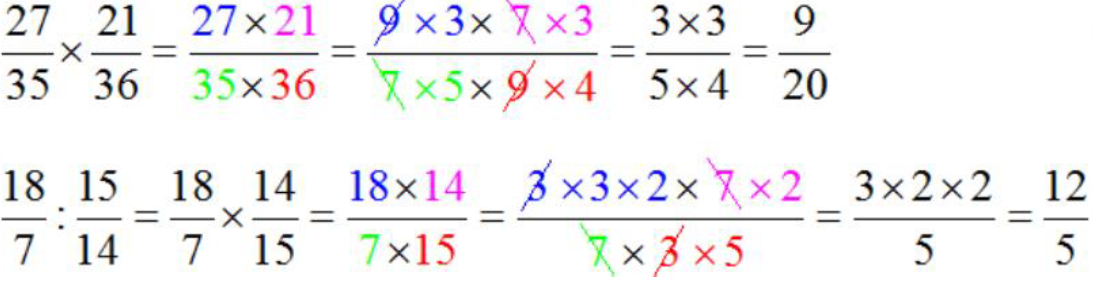
Les pourcentages

Le pourcentage fait forcément référence à une situation de proportionnalité et permet d’exprimer un caractère (40% des ... sont ...) , une augmentation (+5%), une réduction (-50%) , etc.

Le pourcentage noté %, est le rapport d’un nombre, ici noté X, sur une équivalence de 100 :

𝐗 %= 𝐗 ÷ 𝟏𝟎𝟎 = 0,0𝑋 

Prenons un exemple :  𝟒% = 𝟒 ÷ 𝟏𝟎𝟎 = 0,04 

Pour résoudre cette équivalence, nous utiliserons le produit en croix, qui fait toujours référence à une proportionnalité.

Exemples : 

1. La promotion de mon IFSI se compose à 85% de femmes. Sachant que nous sommes une promotion de 130 étudiants, combien de femmes et hommes composent la celle-ci ? Commençons par le nombre de femmes grâce à la proportionnalité de 85% : 

85 ÷ 100 = ?? ÷ 130 soit en appliquant la règle de 3 : (85 X 130) ÷ 100 = 110  La promotion comporte 110 femmes. 

Puis on en déduit le nombre d’hommes : 130 − 110 = 20 La promotion comporte 20 hommes.

 
2. Si le prix d’une formation augmente de 6% sachant qu’elle valait au départ 250€, quel est son nouveau prix ? 

Je vous propose deux méthodes, une par équivalence, l’autre directe :
• 6 ÷ 100= ?? ÷ 250 soit en appliquant la règle de 3 : (6 X 250) ÷ 100 = 15€

• 250 X 0,06 = 15€ 

L’augmentation est de 15€ soit un nouveau prix de la formation de 265€. 

NB : Le rapport ‰ , « pour mille » fonctionne comme le pourcentage mais sur un rapport équivalent à 1000.

Le Rapport Vitesse Distance Temps

Une vitesse se définit comme un rapport entre une distance parcours et le temps mis pour parcourir celle-ci.

Partant de ce constat, nous pourrons en déduire 3 propriétés : 

1. La vitesse moyenne exprimée v d'un objet qui parcours une distance exprimée d pendant une durée t est égale à :  v = d / t 

2. La durée t du parcours d'un objet à la vitesse moyenne v sur une distance d est égale à : t = d / v 

3. La distance d parcourue par un objet à la vitesse moyenne v pendant la durée t est égale à : d = v x t

Comme pour toutes propriétés, il ne faut pas perdre de vue les unités, dans la cadre de ce rapport nous disposons de deux possibilités :

• Le Kilomètre par Heure ( km/h) : une vitesse de 10km/h correspond à la vitesse moyenne (v) d'un objet qui en 1 heure (t) se déplace de 10 kilomètres (d).
• Le Mètre par Seconde (m/s) : une vitesse de 10 m/s correspond à la vitesse moyenne (v) d'un objet qui en 1 seconde (t) se déplace de 10 mètres (d).

Pour convertir une vitesse moyenne d'une norme d'unité à une autre, et puisque 1h = 3600s et que 1km = 1000m , vous pouvez utiliser la simplification suivante :  

V (km/h) = 3,6 x V(m/s)     ou V(m/s) = V(km/h) ÷ 3,6

Exemple : 

Pour se rendre à son stage infirmier, Anaïs mets 45 minutes pour se rendre à 30km. 

A quelle vitesse roule en moyenne Anaïs ? Exprimer la réponse en km/h puis en m/s. 

On sait que le rapport est v = d / t , que l'on nous donne la distance d en km et que 45min = 3/4 d'1 heure soit 0,75.

V = 30 ÷ 0,75 = 40km/h    ; V(m/s) = 40 ÷ 3,6 = 11 m/s 

Lors de son trajet pour se rendre en stage, Anaïs roule à une vitesse moyenne de 40km/h soit 11m/s.

 Résolution d'équations

1. Qu’est-ce qu’une équation ? 

Une équation est une égalité dans laquelle intervient un nombre inconnu, désigné le plus souvent par une lettre minuscule : 𝑥, y, a, b, t

7 + 𝑥 = 15 ; 9,5y = 38 ; t² = 49 ; 𝑥² + 3 = 25 sont des équations.

Résoudre une équation c'est trouver toutes les valeurs possibles du nombre inconnu telles que l'égalité soit vraie, chacune de ces valeurs est appelée une solution de l'équation.

2. Additionner et soustraire

Lorsque l'on ajoute ou que l'on soustrait un même nombre aux deux membres d'une égalité, on obtient une nouvelle égalité.

Si a = b alors a + c = b + c 

Si a = b alors a - c  = b - c

Exemples : 

𝑥 + 9 = 16   ;   𝑥 +9 -9 = 16-9   donc 𝑥 = 6 ; Nous venons de montrer que cette équation admet une seule et unique solution 𝑥.

𝑥 - 6 = 3,5  ;  𝑥 - 6+6 = 3,5 +6  donc 𝑥 = 9,5 ; Nous venons de montrer que cette équation admet une seule et unique solution 𝑥 = 9,5.

3. Multiplication et divisions

Lorsque l'on multiplie ou que l'on divise par un même nombre non nul les deux membres d'une égalité, on obtient une nouvelle égalité : 

Si a = b alors a x c = b x c
Si a = b alors a ÷ c = b ÷ c

Exemples :
5𝑥 = 125 ; (5𝑥) ÷5  = 125 ÷5  donc 𝑥 = 25 ; Nous venons de montrer que cette équation admet une seule et unique solution 𝑥 = 25.

𝑥 ÷ 2 = 73  ; (𝑥 ÷ 2) x2  = 73 x2 donc 𝑥 = 146 ; Nous venons de montrer que cette équation admet une seule et unique solution 𝑥 = 146.

4. Equation avec inconnue des deux côtés

Lorsque l'on se retrouve avec une inconnue de chaque côté de l'équation, la règle est simple : il faut passer toutes les inconnues d'un même côté, le plus simple.

Exemple :
6𝑥 + 40 = 121 - 3𝑥 

6𝑥 + 40+3𝑥 = 121 - 3𝑥 +3𝑥 ; 9𝑥 + 40 = 121

9𝑥 + 40-40 = 121 -40 ;  

9𝑥÷9 = 81÷9   donc 𝑥 = 9 ; Nous venons de montrer que cette équation admet une seule et unique solution 𝑥 = 9.

Résolution de problèmes

Les problèmes sont un ensemble de notions mélangées dans un énoncé, c'est à dire la description d'une mise en situation (généralement en rapport avec les soins infirmiers) , suivi d'une ou plusieurs questions ; Ces questions feront appel à l'ensemble des notions vues ci-dessus.

Le Débit 

Le débit d'un fluide correspond à la quantité de fluide qui s'écoule pendant une durée donnée. 

Comme pour la vitesse vue ci-dessus, il s'agit d'une propriété, ici c'est un volume que l'on divise par une durée (temps d'écoulement) : 

Débit = Volume de fluide écoulé / Temps d'écoulement ;    D = V / t 

Les unités du débit sont celle du Volume en Litre ou m³ , divisé par celle du temps en heure, minute ou seconde. 

Ainsi le débit peut s'exprimer en m³/h , L/h , m³/s , m³/min , mL/min, mL/s ...

Pour passer le débit de m³ aux Litres, quelques équivalences tirées du tableau des unités de mesure sont à connaitre : 

1m³ = 1000L    ;   1dm³ = 1L = 1 000mL   ;   1cm³ = 1mL

Exemple : 

Nous savons que la précédente une poche de 3,5L Nacl du patient a été terminée en 5 heures. 

Quel est le débit de Nacl exprimé en L/h , en mL/h puis en m³/min.

Débit = V / t = 3,5 ÷ 5 = 0,7 L/h

Nous savons qu' 1L équivaut à 1000ml donc 0,7L/h x 1000 = 700mL/h 

Nous savons qu'une heure équivaut à 60 minutes et que 1m³ équivaut à 1000L donc : 

Débit = (  3,5 ÷ 1000 ) ÷  (5 x 60) = 0,0035 x 300 = 1,05 ‬m³/min

Maintenant que je vous ai expliqué l'ensemble des prérequis aux calculs de doses, rentrons dans le concret... comment se mettre à jour, se préparer et devenir un véritable maître des calculs de doses infirmiers ?

En conclusion, quelque soit votre niveau actuel, vous comprenez qu'il y a de nombreuses notions de bases à connaître et maitriser avant même de passer aux calculs de doses, simples puis complexes... Rien ne vaut une bonne révision et pratique pour s'y remettre !  

Pas de secret(s) , il va falloir réviser les prérequis aux calculs de doses, les bases puis passer aux calculs de doses,

...bonne nouvelle, avec des cours simplifiés, méthodes et exercices, c'est facile !

Pour cela, nous vous avons concocté un programme sur mesure pour l'ensemble des notions mathématiques, des prérequis, aux bases jusqu'aux calculs de doses les plus complexes ! 

Premièrement, nous vous accompagnons sur une remise à niveau des prérequis (calculs algébriques, pourcentages, fractions, mesures...) : visionner des cours simplifiés par nos soins, compréhensibles de tous niveaux, retrouver des fiches synthétisant les cours et s'entraîner avec un grand nombre d'exercices.

Deuxièmement, pour chacune des bases des calculs de doses infirmiers ( conversions d'unités, produits en croix, concentrations massique ou en pourcentages, débits en ml ou gouttes) : On reprend les cours  de façon simple, et vous propose un ensemble d'exercices qui se compliquent au fur et à mesure.

Pour aller plus loin dans votre maitrise des calculs, on aborde les calculs de doses dans les soins infirmiers avec les notions les plus complexes (prélèvements de volume, la dilution, les calculs autour des Pousse Seringue Electrique PSE et Pompe PCA) : on explique ces notions qui sont souvent mal comprises des ESIs, décortique des exemples concrets ensemble pour que vous puissiez les maitriser lors de vos partiels.

Pour finir, nous n'avons pas omis tous vos questionnements, vous retrouverez donc nos conseils et bonnes pratiques et des tests pour valider vos acquis.

En bref, Il ne te reste donc plus qu'à passer à l'action en nous rejoignant pour devenir un maître des calculs de doses.

DÉBITS - CONCENTRATIONS - DILUTION - PRÉLÈVEMENTS - PSE - PCA ...

contact@objectif-infirmiere.fr

Liens Utiles

Liens Rapides

© Copyright Objectif-Infirmière™ - Tous droits réservés.

 Mentions légales , Politique de confidentialité , Conditions générales de vente